 |
|
Tags: probability, statistics
The true logic of this world is the calculus of probabilities.
– James Clerk Maxwell
Probability theory is nothing but common sense reduced to calculation.
– Pierre Simon Laplace
The first time I studied probability I didn't like it at all. It was a single semester with the following structure:
Axioms of probability
Combinatorics
Random variables
Distributions
Estimation
Hypothesis testing
After finishing the course I left with the determination of avoiding statistics as much as possible. It felt quite ugly compared with other subjects. It could be in no other way that I ended working constantly with statistics after finishing my degree.
I think one of the reasons I disliked it at first is that reasoning with probabilities feels sometimes like programming in assembly. It's too low level, too much attention to irrelevant details. Sometimes we can apply more higher level data structures, for example Bayesian networks.
The other reason I disliked the course, in retrospective, is that it focused so much on combinatorics and integrals and calculations and so little on reasoning. Most probably this happened because time constraints since it was expected (it's expected, I have just checked) that everything a future aerospace engineer needs to know about statistics is to be learned in one subject. My personal opinion, and I admit I have not taken the usual path, is that it's not the case.
After some talk about the informal concept of probability we started with Kolmogorov's axioms. Here they are in all their glory more or less extracted from Wikipedia. If you have not seen the term \(\sigma\)-algebra before it's just machinery so mathematicians can sleep peacefully at night and you will understand everything that follows ignoring it. If you want to dig deeper (against common sense) there is a short proof in the first chapter of A First Look At Rigorous Probability Theory giving some justification and you can have a look also at Wikipedia.
Let \(\Omega\) be the sample space, \(\Sigma\) a \(\sigma\)-algebra defined on \(\Omega\) and \(P\) a real function with domain \(\Sigma\). Then \(P\) satisfies the following axioms:
First axiom.
For any event \(E \in \Sigma\):
Second axiom.
Third axiom.
For any countable disjoint sequence of events \(E_i \in \Sigma\):
It's unfortunate how they were introduced as “the axioms”. When one introduces axioms it is assumed that everything else will follow from them but they clearly lack something very dear to me which is obviously conditional probability.
Conditional probability
We call \(P (A|B)\) the probability of \(A\) given \(B\) and is defined as the probability that satisfies the equation:
If \(P (B) = 0\) then \(P (A|B)\) is undefined. An analogy I like is that conditioning probability is like zooming on an area of interest and you are basically trying to zoom on a point, you see nothing and can imagine whatever you want. It's very bad luck to condition on an event with \(P (B) = 0\) anyway. It's so bad luck that you should actually check any assumptions you made to calculate your initial probabilities.
At college we did an attempt at justificating the axioms. We first defined intuitive probabilities as the proportion of times an event happens (the frequency of the event). I'm going to put a bar over them to distinguish them from true probabilities:
Where \(E\) is some event, \(n_E\) is the number of times event \(E\) happened and \(n\) is the number of times the experiment was repeated. Then we checked that our intuitive definition of probability agrees with all the axioms and conditional probability. Then we tried to push this more formally through the law of large numbers (LLN) which in its strong form asserts that:
The law of large numbers is a wonderful theorem but the assertion that the above was a justification of the axioms of probability left me completely confused because it looks completely circular!. It would have been great if we could write:
But it's simply not the case. What the LLN is saying instead is that there is some consistency between the probability axioms and our intuitive notion of probability and the fact that we are able to prove it gives some reassurance about their completeness. At best you can argue that the LLN plus the very reasonable assertion that an event with probability 1 is true gives some justification of the axioms but it nevertheless leaves out conditional probability.
Although the axioms are defined on sets and set algebra for good reasons as soon as one tries to solve some exercises it's inevitable to map the axioms to logic: “What's the probability that a fair dice throws a 1 OR a 2?”. And intuitively you learn that:
You can see that it makes perfect sense that \(P (A|B)\) is undefined when \(P (B) = 0\) since starting from something false anything can be true.
My point is that sets are a great framework for rigorous mathematics, measure theory and defining integrals over infinite and complicated event spaces but for my use case forgetting about sets and directly thinking in logic terms is much more natural.
This progression to logic has continued as a result of my work to the point that now I see probabilities as data structures that represent an state of knowledge, the axioms as internal consistency of that representation and conditional probability as the rule adding new information to the data structure.
One consecuence of starting to think in logical terms about probabilities is that you start seeing probability as knowledge representation. Let's illustrate this change of view with a concrete example.
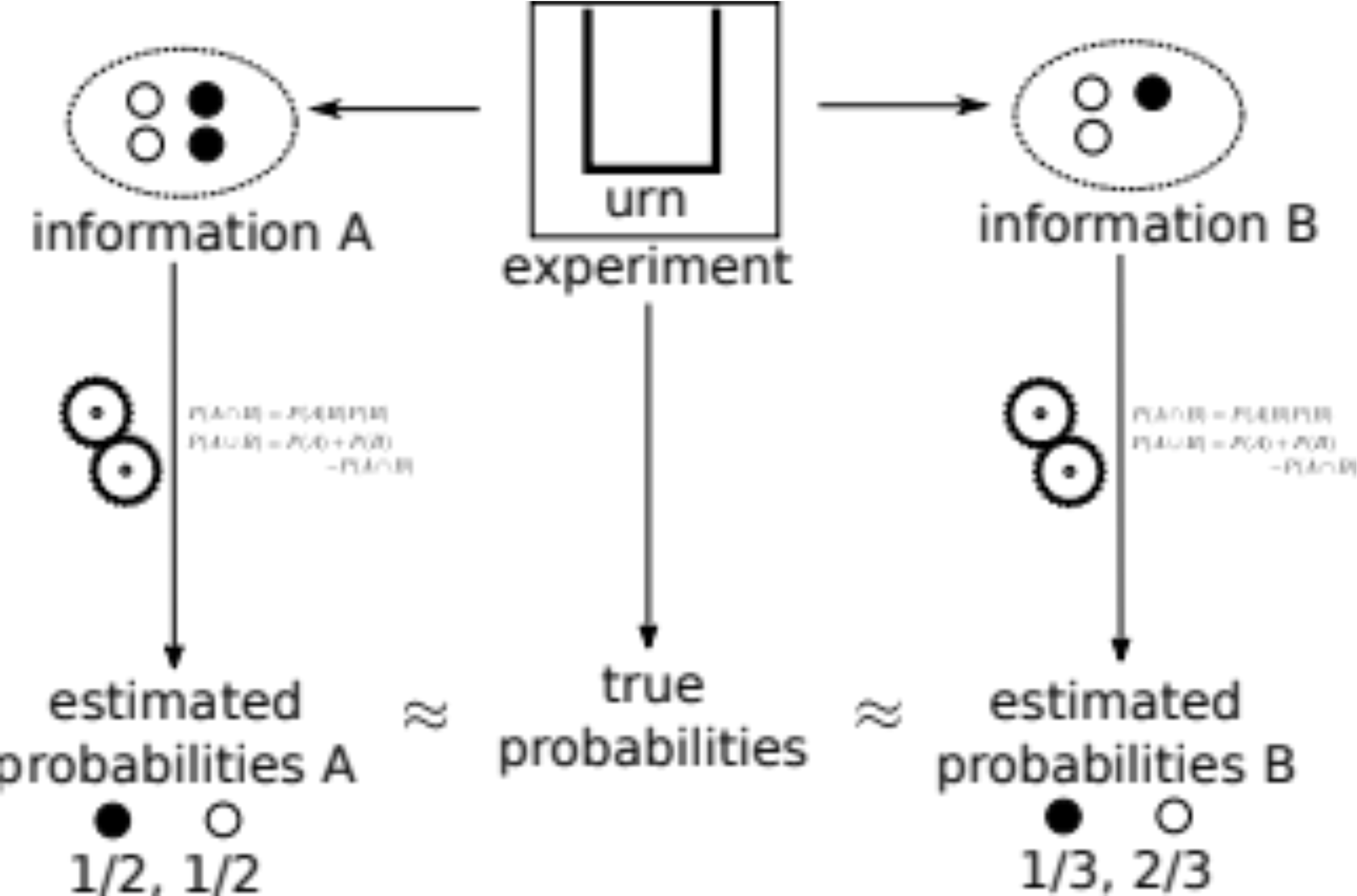
Imagine there is a urn with black and white balls and you are asked about the probability of drawing a black ball. Given no more information the most reasonable answer would be 1/2. Now I tell you that for every black ball there are two white balls. You of course change your probabilities from 1/2 to 1/3.
This is what a believer in objective probability sees:
The experiment is: someone draws a ball from a urn. Based on information about the experiment we compute some probabilities. If the information is correct our estimated probabilities will agree with the true probabilities.
There is a big overlap between people that think of probabilities as frequencies and people that see probabilities as objective maybe because frequency gives a physical process for directly measuring probability. As a matter of fact they usually are put together and simply referred as “frequentists”.
Objective probabilities say that an experiment has probabilities and we as part of some process discover them carrying some computation.
And this is what a believer in subjective probability sees:
The experiment is the same as before. Based on information about the experiment we compute some probabilities the same as before. These probabilities are a mathematical representation of the information we have. It makes no sense to assign probabilities to an experiment since probabilities are assigned to information. We are not able to assign objective probability to an experiment unless the experiment has an objective set of information.
Subjective probabilities say that probabilities are a representation of information. They are subjective because different agents will have different information.
Note that subjective probabilities is not about different people giving whatever probabilities they like since all people with the same information if acting rationally will give the same probabilities. Does this mean that subjective probabilities do not really exist? My personal opinion is that they do exist in the same way that distance or speed exist, it's just that they are relative.
There is also a big overlap between people that use Bayesian methods and believers in subjective probability. They are also usually put together and referred as “bayesians”. The explanation of why is a little more involved and I will leave it out.
Both approaches are equivalent since probabilities in both cases are computed using the same rules based on the same inputs, as you can check in the descriptions. They just differ philosophically on where probabilities live. This however makes differences in the methods used and where hand-waving is moved when giving answers to questions. Frequentists are very nitpicky with their initial assumptions and move the hand-waving to the last moment. Bayesian follow impeccable methods that give solid results but start with dubious initial assumptions.
Hand-waving is inevitable and is the consequence of asking for absolute results from uncertain information. Probability laws don't extract information from vacuum, they just transform information, and if you start with uncertainty you end with uncertainty. The best you can do is as with the LLN, where probability was concentrated to 1 at the cost of an infinite number of information extraction steps (running the experiment) and yet, even in this case, probability was not eliminated. Probability sometimes gets concentrated with information, sometimes disperses as a consecuence of random processes, but never ever dissapears.
Programming a computer to work under uncertainty will almost surely involve storing and updating probabilities somewhere inside the computer's memory. It's almost inevitable that the subjective point of view will take hold of you and I think that the rise in popularity of Bayesian methods has been driven forward by the rise of computers and even more strongly lately by AI. Apart from philosphical considerations Bayesian methods are usually more computationally demanding and computers have also made them more practical.
At some point I discovered that time ago someone gave a proof that the probability axioms are not just logical in the loose sense we have been talking up to this point but that they are actually an extension of logic to uncertain truth in what is known as Cox's theorem. I quite frankly think this is a remarkable result for two good reasons:
It proves that current definition of the probability axioms and conditional probability are inevitable under certain reasonable assumptions. This is the justification I have always looked for.
It opens the possibility to alternate formulations using different assumptions. For example: Can we get probabilities defined on complex numbers? Under what assumptions?
What Cox's theorem says informally is that if a system assigns degrees of certainty, called plausibilities, to uncertain logical propositions, where contradictions are assigned the lowest plausibility and tautologies the highest plausibility, it must do so in such a way that these plausibilities obey the probability laws too.
In my next post I give a full derivation of the theorem.